
How fast does the end of his shadow move? Solution : By similar triangle s - x s = 16 s – 16 x = 6 s 10 s = x Differentiate with respect to t ds dx = dt dt ds = ( 5 ) dt ds/dt = miles/ hour His shadow move at 8 miles/hour 16ft 6ft x s - x sĩ Example :3 One end of a 13 foot – Ladder is on the floor, and the other end rests on a vertical wall. = π r 2 × dr /dt - 1 /2 π r2 = dr / dt Substitute the values of dS/dr & dr/dt in (1) dS / dt = π r × -1/ 2 π r 2 dS / dt = / r when r = 12 ft dS/dt = / 3 ft2/ min The surface of Spherical balloon shrinking at the rate of /3 square feet per minute.Ĩ Example : 2 A man 6 ft tall walks away from a lamp post 16 ft high at the rate of 5 miles per hour. How fast is the surface area shrinking when the radius is 12 ft ? Solution: A sphere of radius r has volume v V = 4/3 π r3 As we know surface area of sphere S S = 4 π r 2 We have to find dS /dt when r = 12 ft here we can see S is independent of time but we can find it in this way dS dS dr = × (1) dt dr dt here S = 4 π r 2 dS/ dr = 8 π r Now for dr /dt : dV / dt = (given) dV dV dr = × (2) dt dr dt V = 4/3 π r3 dV/ dr = π r2 We have many quantities involve rate of change in time shook intensity of earthquakes, inflation of currency, water height of Sea, Stock rates, rate of increase of volume of balloon etc.Ħ Example: 1 Gas is escaping from a spherical balloon at the rate of 2 ft3 / min.
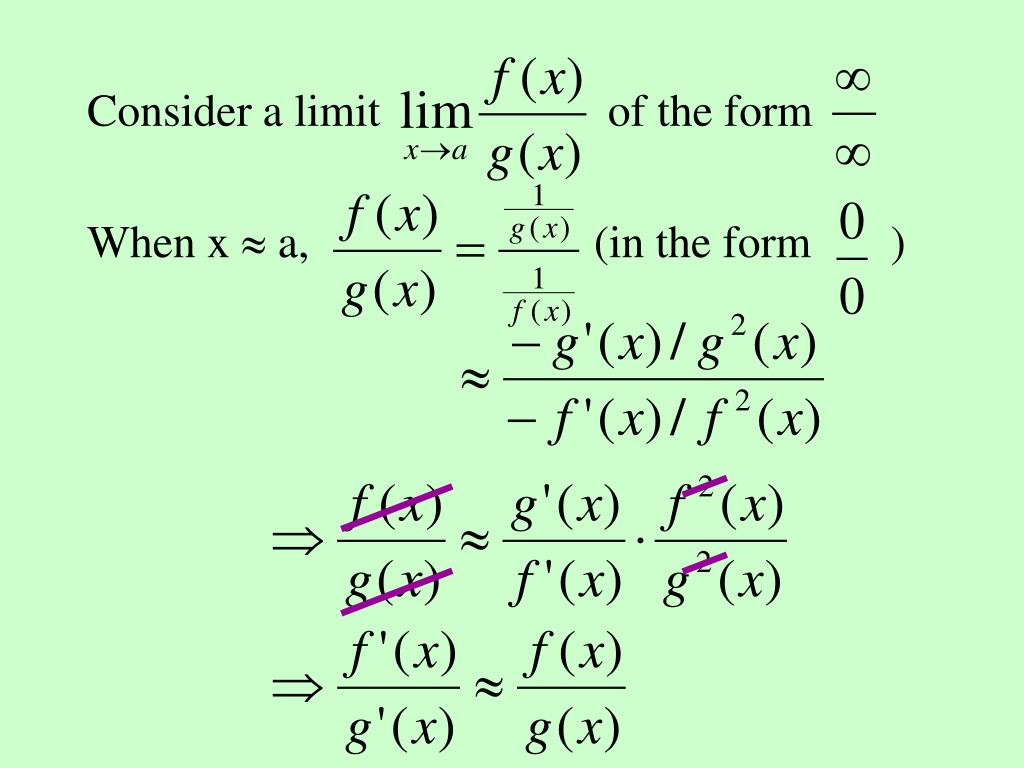
Rate of change of velocity is acceleration. Rate of Change : The derivative of function is a mathematical tool that is used to study rates at which quantity changes. There are two major applications Rate of Change Extreme Valuesĥ 1. Notation īoldface variables such as q =\left.BY ERUM RIAZ Department of Mathematics D.A Degree College For Women Ph-VII (Ext)ģ Analysis : By the end of the lesson students will be able to explain the applications of derivative. It can be understood as a special case of the Hamilton–Jacobi–Bellman equation from dynamic programming. In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. The qualitative form of this connection is called Hamilton's optico-mechanical analogy.

The wave equation followed by mechanical systems is similar to, but not identical with, Schrödinger's equation, as described below for this reason, the Hamilton–Jacobi equation is considered the "closest approach" of classical mechanics to quantum mechanics.


In this sense, it fulfilled a long-held goal of theoretical physics (dating at least to Johann Bernoulli in the eighteenth century) of finding an analogy between the propagation of light and the motion of a particle. The Hamilton–Jacobi equation is the only formulation of mechanics in which the motion of a particle can be represented as a wave. In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.


 0 kommentar(er)
0 kommentar(er)
